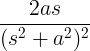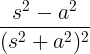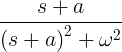Laplace transform table ( F(s) = L{ f(t) } )

Laplace transform converts a time domain function to s-domain function by integration from zero to infinity

of the time domain function, multiplied by e^-st.

The Laplace transform is used to quickly find solutions for differential equations and integrals.

Derivation in the time domain is transformed to multiplication by s in the s-domain.

Integration in the time domain is transformed to division by s in the s-domain.

Laplace transform function

The Laplace transform is defined with the L{} operator:

$F(s)=\mathcal{L}\left \{ f(t)\right \}=\int_{0}^{\infty }e^{-st}f(t)dt$

The inverse Laplace transform can be calculated directly.

Usually the inverse transform is given from the transforms table.

Function name	Time domain function	Laplace transform
Function name	f (t)	F(s) = L{f (t)}
Constant	1	$\frac{1}{s}$
Linear	t	$\frac{1}{s^2}$
Power	tⁿ	$\frac{n!}{s^{n+1}}$
Power	t^a	Γ(a+1) ⋅ s ^-(a+1)
Exponent	e^at	$\frac{1}{s-a}$
Sine	sin at	$\frac{a}{s^2+a^2}$
Cosine	cos at	$\frac{s}{s^2+a^2}$
Hyperbolic sine	sinh at	$\frac{a}{s^2-a^2}$
Hyperbolic cosine	cosh at	$\frac{s}{s^2-a^2}$
Growing sine	t sin at	$\frac{2as}{(s^2+a^2)^2}$
Growing cosine	t cos at	$\frac{s^2-a^2}{(s^2+a^2)^2}$
Decaying sine	e^-atsin ωt	$\frac{\omega }{\left ( s+a \right )^2+\omega ^2}$
Decaying cosine	e^-atcos ωt	$\frac{s+a }{\left ( s+a \right )^2+\omega ^2}$
Delta function	δ(t)	1
Delayed delta	δ(t-a)	e^-as

Property name	Time domain function	Laplace transform	Comment
	f (t)	F(s)
Linearity	a f (t)+bg(t)	aF(s) + bG(s)	a,b are constant
Scale change	f (at)	$\frac{1}{a}F\left ( \frac{s}{a} \right )$	a>0
Shift	e^-at f (t)	F(s + a)
Delay	f (t-a)	e^-asF(s)
Derivation	$\frac{df(t)}{dt}$	sF(s) - f (0)
N-th derivation	$\frac{d^nf(t)}{dt^n}$	sⁿf (s) - s^n-1f (0) - s^n-2f'(0)-...-f^(n-1)(0)
Power	tⁿ f (t)	$(-1)^n\frac{d^nF(s)}{ds^n}$
Integration	$\int_{0}^{t}f(x)dx$	$\frac{1}{s}F(s)$
Reciprocal	$\frac{1}{t}f(t)$	$\int_{s}^{\infty }F(x)dx$
Convolution	f (t) * g (t)	F(s) ⋅ G(s)	* is the convolution operator
Periodic function	f (t) = f (t+T)	$\frac{1}{1-e^{-sT}}\int_{0}^{T}e^{-sx}f(x)dx$